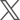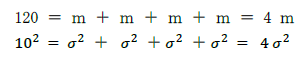緩やかな時刻指定の検討の経緯
前々回（第23回）では配送先が1か所の場合での「延着を許容する緩やかな時刻指定」を、前回（第24回）では「延着に加えて早着を許容する緩やかな時刻指定」について、考えてみた。
今回（第25回）は、「延着を許容する時刻指定（第23回）」を拡張して、複数の配送先に届けるルート配送を対象に、緩やかな時刻指定の効果を考えてみることにする。
なお、詳細については補論で述べることにする。
ルート配送の設定
複数の配送先に届けるルート配送では、あらかじめ到着時刻を指定されていることが多い。たとえば、コンビニの店舗配送では、複数の店舗に効率よく配送できるように、ルートも到着時刻も指定されている。
ここでは、4つの店舗（A1～A4）を順番に回るルート配送を考えることにする。店舗間の走行時間は、平均走行時間が30分で標準偏差が5分の正規分布に従うと仮定する。
このとき、分かりやすくするために納品時間を0分と仮定する。また、余裕時間とは、指定時刻に遅れないために、平均走行時間に加えて余裕を見込む時間である（補論を参照）。
厳密な時刻指定の場合の延着確率（後出、表１を参照）
厳密な時刻指定で延着が許されない場合、30分の平均走行時間だとして、15分の余裕時間を想定し、各配送先で45分の走行時間を見込むものとする。
詳細は補論に譲るが、この場合、4か所のうち１か所以上の配送先で延着する確率は0.52％であり、1年間毎日配送するとしたとき、年に約2日（1.89回）の延着になる。
延着を許容した場合の延着確率（後出、表１を参照）
余裕時間を10分として、各配送先で40分の走行時間を見込んで、各配送先での出発時刻をそれぞれ５分遅くする場合を考える。
この場合、4か所のうち１か所以上の配送先で延着する確率は8.81％であり、1年間毎日配送するとしたとき、年に約32日、月に約2.6回の延着となる。これは実行可能な範囲と考えられる。
なお、余裕時間を5分とした場合、4か所のうち1か所以上の配送先で延着する確率は49.90％となるので、現実的ではないだろう。
時刻指定と待機時間のトレードオフ
以上の分析から明らかになることは、ルート配送における時刻指定が、「すべての配送先で時刻指定を守るために、待機時間が長くなっても、走行時間の余裕を多くとるべき」か、「多少の延着をしても良いので、待機時間を短くするためにも、走行時間の余裕を減らすべき」か、という問題である。
言い換えれば、「厳密な時刻指定・長い待機時間」と「緩やかな時刻指定・短い待機時間」のトレードオフの問題である。そして、「『厳密な時刻指定』と『短い待機時間』の、どちらを効率的と判断するべきか」という問題でもある。
時刻指定と配送先数のトレードオフ
詳細は補論において述べるが、待機時間の減少により、配送先数を増やせる可能性もある。ということは、逆に厳密な時刻指定を貫くことで、配送先数を減らしている可能性もある。
このことは、「厳格な時刻指定・少ない配送先数」と「緩やかな時刻指定・多い配送先数」のトレードオフの問題になる。そして、「『厳密な時刻指定』と『配送先数の増加』の、どちらを優先するのか」という問題でもある。
評価指標で変わる効率性
時刻指定と配送先数がトレードオフの関係にあることは、評価指標（時刻厳守率、待機時間、配送先数など）次第で、効率性の評価が変わることでもある。つまり厳格な時刻指定は、「着荷主にとって、高い時刻厳守率により効率性が高い」とすることもできるが、「輸送業者にとって、長い待機時間や少ない配送先数で効率性が低い」とすることもできる。
もちろん、商取引の内容、配送する商品の内容、配送先（着荷主）の事情、輸送業者の事情などで、評価指標も異なることだろう。
しかし確かなことは、「効率性は評価指標で変わる」ことであり、「何かの効率性を選択することで、別の何かの効率性を捨てているかもしれない」ということである。
＜図1 ルート配送の概念図（配送先4か所の場合）＞
【補論】：数字とグラフで読み解く「物流の課題」
（その10） ルート配送における緩やかな時刻指定の効果
中央大学経済学部教授 小杉のぶ子
ルート配送の設定（図1を参照）
ルート配送において、4か所の配送先 A1、A2、A3、A4を順にまわるとする。
出発地点からA1までの走行時間、A1から A2までの走行時間、A2からA3までの走行時間、A3からA4までの走行時間をそれぞれX1、X2、X3、X4で表す。
これらの走行時間（X1～X4）は互いに独立で、正規分布に従うとする。
ルート配送における平均走行時間（m）と標準偏差（σ）の設定（図2を参照）
いま、走行時間の和 X1+X2＋X3+X4 が、第23回と第24回で扱ったケース（配送先が1か所で走行時間が平均120分、標準偏差10分の正規分布に従うケース）と等しい分布になると仮定する。
このとき、各配送先間の走行時間は平均 m、標準偏差 σ の正規分布に従うことになる。
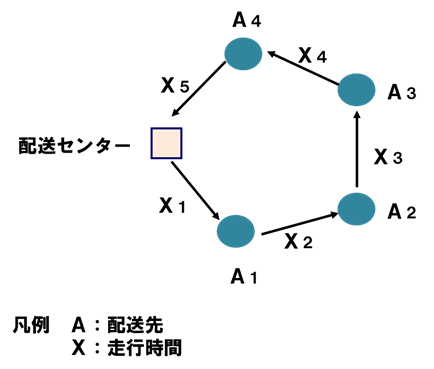
ここで、
が成り立つから、m ＝30、σ2 =25 となり、各走行時間（X1～X4）の分布は平均 m＝30（分）、標準偏差 σ＝ 5（分）の正規分布に従うことがわかる。
なお、荷物の積みおろしに要する時間については考えないこととする。
＜図2 標準正規分布における確率＞
余裕時間の削減による待機時間の減少（図2、表1を参照）
時刻指定を守るための余裕時間と、配送車両の待機時間を考えてみる。
厳密な時刻指定を守るために、それぞれ15分の余裕時間を設けると、4か所の配送先すべてで延着しない（時刻指定を守れる）確率は、 (0.9987)4 で求められ、99.48％となる。このとき、各配送先で45分の走行時間を見込むことになるので、走行時間が平均と同じ30分の場合、各配送先での待機時間は15分となり、4か所なので合計60分の待機時間が発生する。
一方、緩やかな時刻指定として、それぞれ10分の余裕時間を設けると、4か所の配送先で延着しない確率は、(0.9772)4 で求められ、91.19％となる。このとき、各配送先で40分の走行時間を見込むことになるので、走行時間が平均と同じ30分の場合、各配送先での待機時間は10分となり、4か所なので合計40分の待機時間が発生する。
このように、余裕時間を削減できれば、待機時間を減少させることができる。
＜表１ 余裕時間（平均走行時間に加えて余裕を見込む時間）別の「延着しない確率」＞
余裕時間の削減による配送先の増加（図3を参照）
配送センターを出発してから配送後に配送センターに戻るまでの時間をルート配送の所要時間とし、労働時間の上限を4時間（240分）とした場合に、所要時間と配送先数の関係を考えてみる。
いま、配送センターの出発時刻を8時00分として、12時00分までに配送センターに戻るとする。ここで、最終配送先から配送センターへの走行時間は30分とする。なお、図3には、次の配送先に向けて出発する時刻も示している。
ここで、厳密な時刻指定を守るために、配送先それぞれに15分の余裕時間を設けて、各配送先への走行時間を45分とすれば、所要時間は210分（＝45×4＋30）となり、配送先数は4か所になる（図3の(1)）。
緩やかな時刻指定として、配送先それぞれに10分の余裕時間を設けて、各配送先への走行時間を40分とすれば、4か所に配送するときの所要時間は190分（＝40×4＋30）となる。この場合、配送先を増やして5か所にしても、所要時間は230分（＝40×5＋30）となり労働時間の上限を下回る（図3の(2)）。
このとき、5か所すべての配送先で延着しない（時刻指定を守れる）確率は、(0.9772)5 で求められ、89.11％となる。よって、延着確率 10.89 %（＝ 1－0.8911）を許容できれば、配送先を１か所増やして、4か所から5か所にすることができる。
＜図3 厳密な時刻指定と緩やかな時刻指定の比較＞
連載 物流の読解術 第24回：早着と延着を許容する時刻指定 －物流の効率化を考える(3)－
