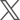物流の効率化と時刻指定
前回(第22回)では、「物流の需給バランスの維持」という視点での「効率化」が重要であることを示した。今回(第23回)からは、効率化にまつわる様々な話題を示しながら、効率化の考え方を整理してみたいと思う。
今回取り上げるのは、配送時の時刻指定である。従来の時刻指定は、着荷主(配送先)のニーズに合わせた「厳密な時刻指定」だった。しかし、「荷主と物流事業者の間の需給バランス」が重要な時代になると、物流事業者の都合も含めた「延着を許容する時刻指定」へと変わる可能性がある。
時刻指定の2つの考え方
時刻指定について、大別すると2つ(荷主、物流事業者)の考え方がある。
荷主としては、到着時刻が決まっていれば円滑な入出庫管理が可能になるので、「厳密な時刻指定こそ、ロジスティクスの効率化に貢献する」という考え方になるだろう。
物流事業者としては、時刻指定を確実に守ろうとすれば、「目標到着時刻を早めに設定することで待機時間が長くなってしまうため、物流事業者(納品業者、輸送業者など)の効率は下がる」というものである。
つまり、「荷主にとっての効率化が、物流事業者にとっては非効率(先回りして出発して現地で待機する)を生む」という皮肉な現実に直面することも多い。
時刻指定と待機時間の関係
時刻指定と待機時間の関係を考えるために、以下のような「時刻指定の状況」を仮定してみる。
貨物車による配送において、到着の時刻指定が9時で平均走行時間が2時間のとき、7時に出発すると2回に1回は遅刻してしまう。このため、渋滞に備えて30分早く6時30分に出発すれば、30分遅延しても指定時刻に間に合うはずである。しかし、6時30分に出発すると、走行時間が平均と同じ2時間であれば8時30分に到着するので、待機時間は30分となる。もしも、走行時間が1.5時間のときは、1時間待機することになる(図1)。
先述したように、荷主の効率性を追求する「時刻指定」が、物流事業者にとっては不測の事態に備えた「余裕時間」を必要とし、この「余裕時間」が「ムダな待機時間」となって通常時には非効率をもたらす。この物流事業者の非効率が運転手不足や車両不足に拍車をかければ、巡り巡って荷主の非効率に結びつくブーメランにもなってしまう。
さらに、待機車両がアイドリングしながら停車していれば、渋滞を起こしたり排ガスや騒音をまき散らすことにもなる。
「緩やかな時刻指定」の可能性
すでに示したように、荷主のニーズだけを優先して厳密な時刻指定を守ろうとすれば物流事業者の待機時間が増えてしまい、社会的な悪影響を引き起こす可能性もある。これを回避するためには、荷主と物流事業者の歩み寄りという視点で、緩やかな時刻指定(多少の延着や早着を許容する時刻指定)を検討すべきだろう。
もちろん、多少在庫を増やせば延着を許容できる場合もあれば、鮮魚のセリのように延着が認められない場合もあるだろう。だからこそ、指定時刻を守ることができない延着の確率を考えながら、どの程度の確率の場合にどの程度の延着を認めるべきかが、重要な課題になるはずである。
今回の補論では、上記の視点から延着の確率を考慮しながら「延着を許容する時刻指定」について考えてみることにする。

【補論】:数字とグラフで読み解く「物流の課題」
(その8) 延着を許容する時刻指定の効果
中央大学経済学部教授 小杉のぶ子
時刻指定と余裕時間
荷主(着荷主)の厳密な時刻指定が、物流事業者にとっては不測の事態に備えた時間の余裕を必要とし、この余裕が通常時にはムダ(非効率)となる。
貨物車の走行時間を考えたとき、平均で2時間かかる場合、渋滞がなければ1時間30分で到着することもあるが、渋滞に巻き込まれると2時間30分かかることもある。ここで走行時間の分布は、正規分布に従うと仮定して考えていくことにする。
このとき、時刻指定を守るために、走行時間を2時間30分と想定しておけば延着はほとんどなくなる。しかし、走行時間が平均と同じ2時間であれば、30分の待機時間が発生する。
正規分布の性質(図2を参照)
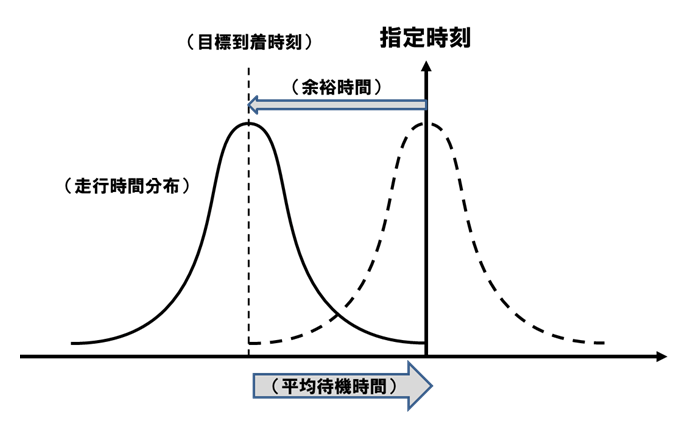
正規分布とは、山が一つで平均値を中心に左右対称の釣鐘型になっている分布である。このグラフと横軸との間の面積の合計は1であり、この面積が確率を表す。
正規分布では、グラフの形が尖っていようとなだらかであろうと、平均値から標準偏差(データが平均値からどれくらい散らばっているかを示す指標)の定数倍までの範囲に値をとる確率は決まっている。いま、平均値を m、標準偏差を σ で表す。
たとえば、データが「m から m+σ の間」に値をとる確率は34.13%である。(すなわち、正規分布のグラフと横軸で囲まれた図形のうち、m から m+σ までの間の面積が0.3413である。)同様に面積をみていくと、「m+σ から m+2σ の間」に値をとる確率は13.59%、「m+2σ から m+3σ の間」に値をとる確率は2.15%、「m+3σ 以上」の値をとる確率は0.13%である。
走行時間の分布の特徴(図2を参照)
これ以降は、貨物車の走行時間が平均2時間、標準偏差10分の正規分布に従う場合を考える。このとき、正規分布の性質から、「実際の走行時間と平均値との差が生ずる確率はどのくらいか」を考えることができる。
仮定より、平均走行時間 m=120分、標準偏差 σ=10分である。このとき、貨物車が出発後2時間(120分)から2時間10分(130分)の間に到着する確率は34.13%、1時間50分(110分)から2時間(120分)の間に到着する確率も34.13%である。ということは、出発してから2時間の前後10分間の時間帯(110~130分)に到着する確率は68.26%となる。同様に2時間の前後20分間の時間帯(100~140分)に到着する確率は95.44%(=(0.3413+0.1359)×2)となる。
次に、「走行時間が〇分以内、あるいは〇分以上となる確率」を考えてみよう。貨物車が出発してから2時間10分(130分)以内に到着する確率は、「m+σ」の左側部分の合計なので、84.13%であり、2時間10分(130分)以上かかる確率は、「m+σ」の右側部分の合計なので15.87%である。同様に、出発してから2時間20分(140分)以内に到着する確率は、「m+2σ」の左側部分の合計なので97.72%であり、2時間20分(140分)以上かかる確率は、「m+2σ」の右側部分の合計なので2.28%である。
延着を認める「緩やかな時刻指定」(図3を参照)
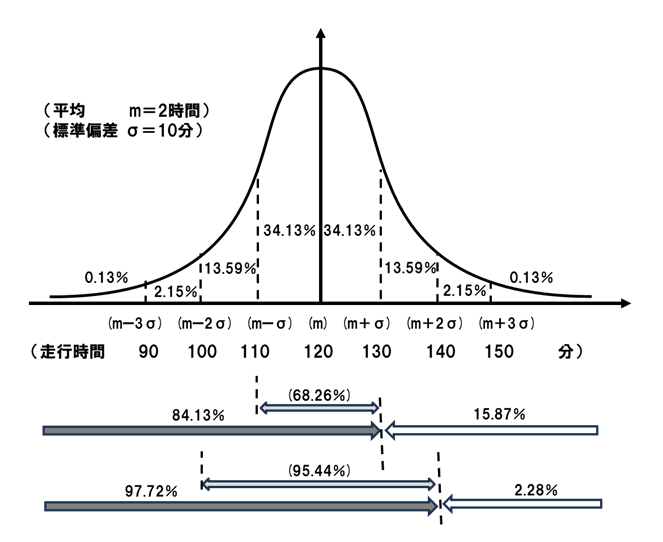
貨物車による配送において、到着時刻が9時に指定されているとする。走行時間は上述のとおり、平均120分、標準偏差10分の正規分布に従っている。
厳密な時刻指定とは、「一度たりとも遅れは認めない」ということだと考えると、到着指定時刻である9時の150分(=m+3σ)前である6時30分に出発することになる。このとき、延着確率は0.13%、すなわち1000回に1.3回なので、1年間毎日(365回)配送している場合は年に0.5回程度の頻度しか遅れないことになる(図3(1)の6:30出発の場合)。
次に、「多少の延着を認める」ということで、「何回かに1回は遅れてもよい」とする場合を考える。このとき、もしも、「100回に2~3回程度の遅れは認める」となると、指定時刻9時の140分(=m+2σ)前である6時40分に出発すればよい。このとき、9時00分までに到着する確率は97.72%なので、延着確率は2.28%、すなわち月に0.68回程度(年に8.3回程度)の頻度となる。延着する場合の内訳をみると、9時00分から9時10分までの間に到着する確率は2.15%、9時10分以降に延着する確率は0.13%である(図3(2)の6:40出発の場合)。
さらに、「100回に16回程度の遅れは認める」となると、指定時刻9時の130分(=m+σ)前である6時50分に出発すればよい。このとき、9時00分までに到着する確率は84.13%なので、延着確率15.87%、すなわち週に1.1回程度(月に4.8回程度)の頻度となる。延着する場合の内訳をみると、9時00分から9時10分までの間に到着する確率が13.59%、9時10分以降の延着確率は2.28%である(図3(3)の6:50出発の場合)。
「延着を認める時刻指定」の効果
以上からもわかるように、「絶対に遅れてはいけない(延着確率0.13%)」とすることにより、貨物車の出発時刻をかなり早めて6時30分にしなければならなくなり、これに伴い待機時間が増えてしまうことになる。そこで、月に0.68回程度の遅れを認めることで、出発時刻を10分遅らせて6時40分にすることができる。さらに、週に1.1回の遅れも認めることができるのならば、出発時刻を20分遅らせて6時50分にすることができる。
このように、多少の延着を認めることで出発時刻を遅らせることができ、待機時間を減らすことができるのであるが、この場合でも実は高い確率で貨物車は指定された時刻に間に合うことがわかる。
「早着時の早期納品受付け」の効果
上記のとおり、延着を認めることで待機時間を削減できるが、延着を認めない代わりに、指定時刻よりも前から納品を受付けることで、待機時間を削減する方法もある。
いま、図3の(1)(厳密な時刻指定)において、指定時刻(9時)の10分前である8時50分から納品を受付ける場合を考える。この場合、8時50分までに車両が到着している確率は97.72%と非常に高いことから、この時間から納品受付けが可能となれば、これらの車両は9時まで待機する必要がなくなり、97%以上の確率で待機時間を10分削減できることなる。
連載 物流の読解術 第22回:効率化をめぐるパラダイムシフト -物流の効率化を考える(1)-