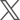直線型配送（配送経路が束ねられている場合）での共同化の例
配送は、多くの着地（配送先）に貨物を配ることなので、つい平面的に移動することを思い浮かべてしまう。たとえば、共同配送センターで店舗別の品揃えや小分けをしてから、複数の店舗に配送する例である。
しかし配送と一口に言っても、宅配便のように品揃えをする必要がなく、しかも直線的に移動するような場合には、共同配送も導入しやすくなる（図１）。
たとえば、複数の着地（配送先）が、半島の先にあるような場合である。類似した例としては、離島、山間地、都心の高層ビルなどがある。これらの場合、通過せざるを得ない場所として、半島では付け根部分の都市、離島では航路のある港、山間地では道路が始まる山麓の都市、高層ビルでは地下の駐車場や荷さばき場などがある、このような直線型の配送では、通過せざるを得ない場所において積替え場所を用意しておけば、直送と共同配送の使い分けが容易となる。
このような共同配送は、昔から離島や中山間地域への輸送には、他社に委託する輸送（「差し込み」などと言われている）が存在していたから、決して現代に始まった新しい工夫ということでもない。
共同配送に有利な直線型配送
先の第16回で、共同配送に有利な条件として、(1)荷揃えや小分けがあるとき、(2)積載率が低いとき、(3)遠回りでもよいとき、(4)配送密度が高いとき、(5)到着台数を減らしたいときなどを示した。
直線型の配送を考えてみると、(1)荷揃えや小分けについては、配送経路の途中で、必要に応じて共同配送センターに寄ればよい。(2)積載率については、低ければ共同配送を選択し、満載であれば直送する。(3)遠回りについては、直線型の配送の配送経路は束ねられているので、共同配送になっても走行距離が増加することは少ない。(4)配送密度については、配送経路が束ねられていると、着地（配送先）の密度も高い。(5)到着台数は、積載率に応じて積替えることで、削減の可能性が高い。
直線型配送における共同配送の選択の考え方
直線型配送で配送経路が束ねられている場合には、経路の途中に共同配送センターがあるのだから、貨物が満載であれば共同配送センターで積替えずに直送した方が費用は小さいだろう。逆に、低積載であれば、共同配送センターに立ち寄って配送を委託（共同配送の利用）したほうが費用は小さいはずである。
そこで、今回の補論では、直送と委託の費用の比較にもとづく共同配送の選択について、考えることにする。
＜図１ 直線型配送における共同配送の例＞
【補論】：数字とグラフで読み解く「物流の課題」
（その4） 直線型配送における直送と共同配送の比較
中央大学経済学部教授 小杉のぶ子
今回（第17回）は、直線型配送における直送と共同配送を比較するために、問題を単純化して考える。具体的には、Ａ社が貨物を輸送する際に、「自社で直送」、または「Ｂ社に委託」のどちらかを選択すると考えることにする。ここで、直送とは「自らが最終着地（配送先）まで貨物を届けること」であり、共同配送とは「輸送途中で、他社に貨物の輸送を委託すること」とする。
このとき、輸送を自社で行った場合と委託した場合の費用の大小によって、直送と共同配送の選択は変わることになる（図２参照）。たとえば、輸送途中で荷揃えが不要で、かつ貨物が満載のときには直送を選択することになるであろう。また、荷揃えが必要なときや低積載のときには、共同配送（他社に委託）を選択すると考えることができる。
＜図２ 直線型配送における直送と共同配送の比較＞
直送と共同配送（委託）の選択をグラフで解く場合に、以下のように考えることができる。
(1) 直送と共同配送（委託）では、輸送費が小さい方を選択することとする。
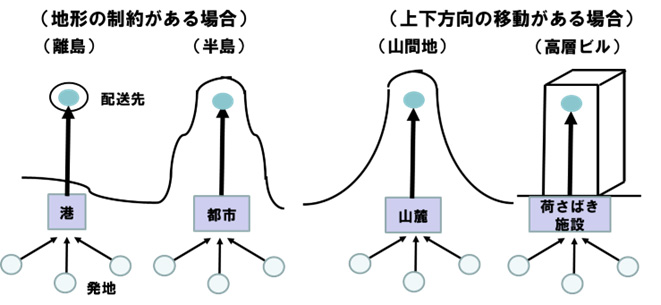
(2) 直送とは、発地から着地まで（距離 d1+d2 ）をＡ社が自社輸送することである。
(3) 直送の場合、発地から着地までのＡ社の輸送費（ b0 ）は、配送個数にかかわらず一定とする。
(4) 共同配送（委託）とは、発地から共同配送センターまで（距離 d1 ）をＡ社が自社輸送し、共同配送センターから着地まで（距離 d2 ）をＡ社がＢ社に委託することである。
(5) 共同配送（委託）の場合、発地から共同配送センターまで（距離 d1 ）を自社で輸送する費用（ b1 ）は配送個数にかかわらず一定であると仮定する。共同配送センターから着地まで（距離 d2 ）の委託費は、１個当たりの委託費（ a ）と配送個数（ x ）で決まるとする。
この結果、直送と共同配送の費用は、以下の式で表すことができる。
（直送の費用） = b0
（共同配送の費用）= b1+ax
ここで、b0：発地から着地までＡ社が自社輸送するときの費用
b1：発地から積替地までＡ社が自社輸送するときの費用
a：１個当たりの委託費
x：配送個数
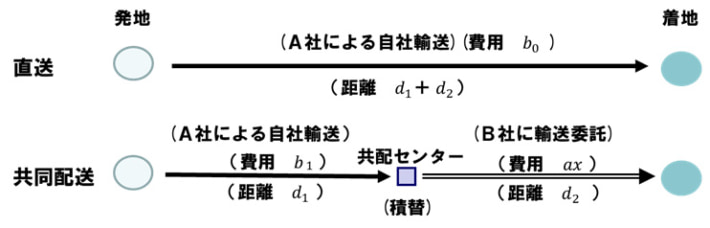
直送と共同配送の選択は、この２つの式を比較して、費用の小さい方を選べばよい。具体的には、図３の２直線の交点を境に、費用の小さい方を選択すればよいことになる。
＜図３ 直線型配送における共同配送の選択＞
